In link, I showed that we could approximate the randomness of a stochastic process using a set of scenarios. A scenario is a potential realization of a multivariate random variable. A large variety of different methods have been suggested for the generation of scenarios. They range from using simple historical returns to more complex methods based on random sampling from historical data (Bootstrap methods) and Monte Carlo simulation, as well as forecasting methods link.

In general, a set of scenarios approximating a stochastic process of financial returns can be described using an index $s$ associated to each scenario, with $s = 1, ... , S$ , where $S$ is the total number of scenarios. Given $n$ assets, a scenario consists of $n$ return realizations, one for each asset. The $s'th$ realization is the rate of return of asset $i$ under scenario $s$ . A portfolio’s expected return and risk is then to be evaluated on $S$ mutually exclusive scenarios $s = 1, ... , S$ , each of which occurring with a probability $p_s$

An inherent problem of scenario generation is the dimensionality of the approximation of the continuous stochastic process. In order to get a good approximation of the underlying process, a large number of scenarios is needed which in turn increases the size of the asset allocation problem. Two overall contrasting approaches exist when addressing this problem, i.e. scenario reduction techniques and moment matching. Both try to reduce the number of scenarios while preserving the overall structure. While both approaches have merits, link compare the two methods in the context of financial optimization, and find (when ensuring the absence of arbitrage in the scenarios) that moment matching provides superior solutions compared to scenario reduction.

The moment matching technique works by approximating the statistical moments (mean, standard deviation, skewness, kurtosis and correlation) of the original set of scenarios using a reduced number of scenarios. The statistical moments are assumed to be the “true” moments of the stochastic process, and the method then seeks to approximate these moments. In practice, this is done by minimizing the squared difference between the “true” moments and the moments of the reduced scenarios. This is in some ways similar to estimating the parameters in linear regression, where we minimize the squared residuals. The moment matching problem can be written as

$\min \ (mu^* - mu_s)^2 + (sd^* - sd_s)^2 + (skew^* - skew_s)^2 + (kur^* - kur_s)^2 + (corr^* - corr_s)^2$

where $*$ denote the “true” statistical moments and $s$ denotes the statistical moments of our scenarios. This method can be conveniently implemented in Python using the optimization routines in the excellent SciPy library.

To show the application of the algorithm, let’s download historical price data for S&P500 and an aggregated bond index proxied by the ETFs SPY and AGG. First, I compute the statistical moments: mean, standard deviation, skewness, kurtosis, and covariance. These are assumed to be the “true” moments that we seek to match with N scenarios. We set N = 50, and run the moment matching algoritm. The minimization function requires an initial guess on the starting parametes. We use the multivariante normal distribution as initial guess, which is probably not too far off assuming the we do not have extreme skewness or kurtosis.

The resulting moment matched distribution is plotted below together with the historical monthly returns, where the yellow dots are our moment matched scenarios and the blue dots are the historical returns.

CVAR

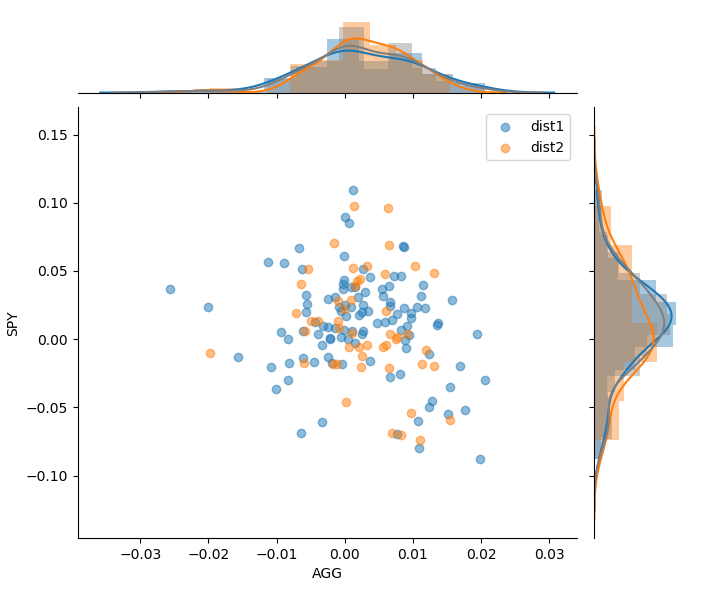
From the density plots and correlation structure, we can observe that our moment matched scenarios are quite close to the original structure, despite only using less than half the amount of scenarios. Though, one problem with this approach remains: the optimization problem is highly non-linear and is quite dependant on having good starting parameters.

Code

Download of Data and CVaR Optimization

import pandas as pd
import numpy as np
from pandas_datareader import data
import seaborn as sns
import matplotlib.pyplot as plt
from scipy.optimize import minimize
from scipy.stats import skew, kurtosis

# We would like all available between these dates.
start_date = '2010-01-01'
end_date = '2018-12-31'

# tickers
tickers = ["SPY","AGG"]

# User pandas_reader.data.DataReader to load the desired data.
panel_data = data.DataReader(tickers, 'yahoo', start_date, end_date)
df_close = panel_data["Adj Close"]

# Daily returns, and remove the first row as it is NA
df_ret = df_close.resample('M').last().pct_change().iloc[1:]

# define "True" moments
mu_ = df_ret.mean().values
std_ = df_ret.std().values
skew_ = df_ret.skew().values
kur_ = df_ret.kurtosis().values
cov_ = df_ret.cov().values

# ini moment matching algorithm
MM = MomentMatch()
# input parameters
Para_match = np.array([mu_,std_,skew_,kur_,[cov_] ])
# find a reduced number of scenarios with approx same statistical moments
MM_scen = MM.MomentMatching(Para_match=Para_match)

Functions for moment matching

class MomentMatch:
    
    def MomentMatchingFunc(self,x,Para_match):
        """ Moment maching function. Create a discrete approximitation of a finite set of statistical moments using a defined number of scenarios
        
        Parameters
        ----------
        x : dict
            Scenarios (variables)
        Para_match : numpy array
            statistical moments to be matched    
        
        Returns
        -------
        float
            returns the error of the approximation
       
        References
        ----------
            .. [1] Hoyland, Kjetil, Michal Kaut, and Stein W. Wallace. A heuristic for moment-matching scenario generation. Computational optimization and applications 24.2-3 (2003): 169-185.
        """
        # true moments
        exp_mu = Para_match[0]
        exp_sds = Para_match[1]
        exp_skew = Para_match[2]
        exp_kur = Para_match[3]
        exp_cov_m = Para_match[4][0]

        # get correlation matrix from covariance matrix
        std_ = np.sqrt(np.diag(exp_cov_m))
        exp_cor_m = exp_cov_m / np.outer(std_, std_)

        # create scenarios
        xx = np.reshape(x, (-1, len(exp_mu)))

        # moments of the scenarios
        m1 = np.mean(xx,axis=0)
        m2 = np.std(xx,axis=0)
        m3 = [skew(xx[:,i]) for i in range(len(exp_mu)) ]
        m4 = [kurtosis(xx[:,i]) for i in range(len(exp_mu)) ]

        # sum of sum of squared residuals
        epsilon = sum( m1 - exp_mu )**2 + sum( m2 - exp_sds)**2 + sum( m3 - exp_skew)**2 + sum( m4 - exp_kur)**2 + sum(sum( (np.corrcoef(xx,rowvar=False)-(exp_cor_m))**2))

        return(epsilon)

    def MomentMatching(self,Para_match,S_N=50,silent=False):
        """ Moment Matching method, which minimize the error term between an approximation and the defined moments. The method starts by initializing the parameters using a normal distribution
        
        """
        # get covariance matrix
        covar = Para_match[4][0]
        # get starting parameters using a random normal distribution
        x_ini = np.random.multivariate_normal(Para_match[0],covar,S_N).ravel() # initial guess is a multivariate normal distribution

        # minimize the residuals
        res = minimize(self.MomentMatchingFunc, x_ini, method='CG',args=(Para_match)) # method="CG",options={'maxiter':60, 'disp': silent} 

        # get results and format them as a matrix
        scen = np.reshape(res.x, (-1, len(Para_match[0])))

        return(scen)